Poseidon2

Poseidon2 is a recently released optimized version of Poseidon. The two versions differ in two crucial points. First, Poseidon is a sponge hash function, while Poseidon2 can be either a sponge or a compression function depending on the use case. Secondly, Poseidon2 is instantiated by new and more efficient linear layers with respect to Poseidon. These changes decrease the number of multiplications in the linear layer by up to 90% and the number of constraints in Plonk circuits by up to 70%. This makes Poseidon2 currently the fastest arithmetization-oriented hash function without lookups. Since the compression mode is efficient it is ideal for use in Merkle trees as well.

An overview of the Poseidon2 hash is provided in the diagram below

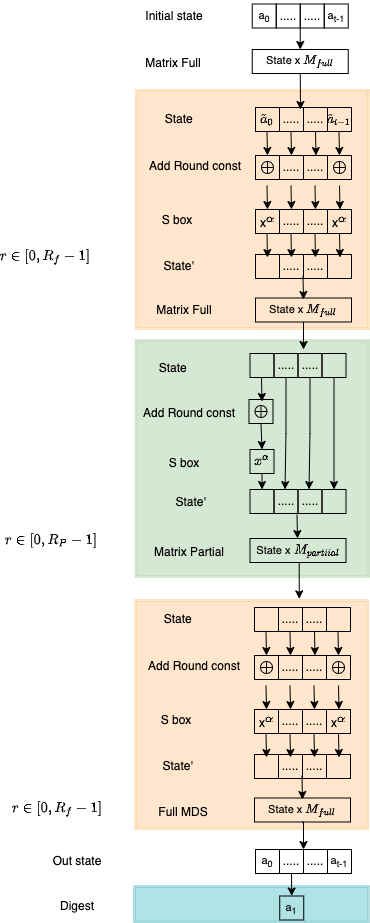
Description

Round constants

• In the first full round and last full rounds Round constants are of the structure $[c_0,c_1,\ldots , c_{t-1}]$, where $c_i\in \mathbb{F}$
• In the partial rounds the round constants is only added to first element $[\tilde{c}_0,0,0,\ldots, 0_{t-1}]$, where $\tilde{c_0}\in \mathbb{F}$

Poseidon2 is also extremely customizable and using different constants will produce different hashes, security levels and performance results.

We support pre-calculated constants for each of the supported curves. The constants can be found here and are labeled clearly per curve <curve_name>_poseidon2.h.

You can also use your own set of constants as shown here

S box

Allowed values of $\alpha$ for a given prime is the smallest integer such that $gcd(\alpha,p-1)=1$

For ICICLE supported curves/fields

• Mersene $\alpha = 5$
• Babybear $\alpha=7$
• Bls12-377 $\alpha =11$
• Bls12-381 $\alpha=5$
• BN254 $\alpha = 5$
• Grumpkin $\alpha = 5$
• Stark252 $\alpha=3$

MDS matrix structure

There are only two matrices: There is one type of matrix for full round and another for partial round. There are two cases available one for state size $t'=4\cdot t$ and another for $t=2,3$.

$t=4\cdot t'$ where $t'$ is an integer

Full Matrix $M_{full}$ (Referred in paper as $M_{\mathcal{E}}$). These are hard coded (same for all primes $p>2^{30}$) for any fixed state size $t=4\cdot t'$ where $t'$ is an integer.

5 & 7 & 1 & 3 \\ 4& 6 & 1 & 1 \\ 1 & 3 & 5 & 7\\ 1 & 1 & 4 & 6\\ \end{pmatrix}

As per the paper this structure is always maintained and is always MDS for any prime $p>2^{30}$.

eg for $t=8$ the matrix looks like

$$M_{full}^{8\times 8} = \begin{pmatrix} 2\cdot M_4 & M_4 \\ M_4 & 2\cdot M_4 \\ \end{pmatrix}$$

Partial Matrix $M_{partial}$(referred in paper as $M_{\mathcal{I}}$) - There is only ONE partial matrix for all the partial rounds and has non zero diagonal entries along the diagonal and $1$ everywhere else.

$$M_{Partial}^{t\times t} = \begin{pmatrix} \mu_0 &1 & \ldots & 1 \\ 1 &\mu_1 & \ldots & 1 \\ \vdots & \vdots & \ddots & \vdots \\ 1 & 1 &\ldots & \mu_{t-1}\\ \end{pmatrix}$$

where $\mu_i \in \mathbb{F}$. In general this matrix is different for each prime since one has to find values that satisfy some inequalities in a field. However unlike Poseidon there is only one $M_{partial}$ for all partial rounds.

$t=2,3$

These are special state sizes. In all ICICLE supported curves/fields the matrices for $t=3$ are

$$M_{full} = \begin{pmatrix} 2 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 2 \\ \end{pmatrix} \ , \ M_{Partial} = \begin{pmatrix} 2 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 3 \\ \end{pmatrix}$$

and the matrices for $t=2$ are

$$M_{full} = \begin{pmatrix} 2 & 1 \\ 1 & 2 \\ \end{pmatrix} \ , \ M_{Partial} = \begin{pmatrix} 2 & 1 \\ 1 & 3 \\ \end{pmatrix}$$

Supported Bindings

Rust

Rust API

This is the most basic way to use the Poseidon2 API. See the examples/poseidon2 folder for the relevant code

let test_size = 4;
let poseidon = Poseidon2::new::<F>(test_size,None).unwrap();
let config = HashConfig::default();
let inputs = vec![F::one(); test_size];
let input_slice = HostSlice::from_slice(&inputs);
//digest is a single element
let out_init:F = F::zero();
let mut binding = [out_init];
let out_init_slice = HostSlice::from_mut_slice(&mut binding);

poseidon.hash(input_slice, &config, out_init_slice).unwrap();
println!("computed digest: {:?} ",out_init_slice.as_slice().to_vec()[0]);

Merkle Tree Builder

You can use Poseidon2 in a Merkle tree builder. See the examples/poseidon2 folder for the relevant code.

pub fn compute_binary_tree<F:FieldImpl>(
    mut test_vec: Vec<F>,
    leaf_size: u64,
    hasher: Hasher,
    compress: Hasher,
    mut tree_config: MerkleTreeConfig,
) -> MerkleTree
{
    let tree_height: usize = test_vec.len().ilog2() as usize;
    //just to be safe
    tree_config.padding_policy = PaddingPolicy::ZeroPadding;
    let layer_hashes: Vec<&Hasher> = std::iter::once(&hasher)
        .chain(std::iter::repeat(&compress).take(tree_height))
        .collect();
    let vec_slice: &mut HostSlice<F> = HostSlice::from_mut_slice(&mut test_vec[..]);
    let merkle_tree: MerkleTree = MerkleTree::new(&layer_hashes, leaf_size, 0).unwrap();

    let _ = merkle_tree
        .build(vec_slice,&tree_config);
    merkle_tree
}

//poseidon2 supports t=2,3,4,8,12,16,20,24. In this example we build a binary tree with Poseidon2 t=2.
let poseidon_state_size = 2;
let leaf_size:u64 = 4;// each leaf is a 32 bit element 32/8 = 4 bytes

let mut test_vec = vec![F::from_u32(random::<u32>()); 1024* (poseidon_state_size as usize)];
println!("Generated random vector of size {:?}", 1024* (poseidon_state_size as usize));
//to use later for merkle proof
let mut binding = test_vec.clone();
let test_vec_slice = HostSlice::from_mut_slice(&mut binding);
//define hash and compression functions (You can use different hashes here)
//note:"None" does not work with generics, use F= Fm31, Fbabybear etc
let hasher :Hasher = Poseidon2::new::<F>(poseidon_state_size.try_into().unwrap(),None).unwrap();
let compress: Hasher = Poseidon2::new::<F>((hasher.output_size()*2).try_into().unwrap(),None).unwrap();
//tree config
let tree_config = MerkleTreeConfig::default();
let merk_tree = compute_binary_tree(test_vec.clone(), leaf_size, hasher, compress,tree_config.clone());
println!("computed Merkle root {:?}", merk_tree.get_root::<F>().unwrap());

let random_test_index = rand::thread_rng().gen_range(0..1024*(poseidon_state_size as usize));
print!("Generating proof for element {:?} at random test index {:?} ",test_vec[random_test_index], random_test_index);
let merkle_proof = merk_tree.get_proof::<F>(test_vec_slice, random_test_index.try_into().unwrap(), false, &tree_config).unwrap();

//actually should construct verifier tree :)
assert!(merk_tree.verify(&merkle_proof).unwrap());
println!("\n Merkle proof verified successfully!");